DIETMAR GUDERIAN*
TRANSFORMATIONEN
Aus dem Raum zu Ebene und Zeit
„Das Phänomen Kraft kann nicht unmittelbar sehbar gemacht werden.
Nur über die Wechselbeziehung zwischen Kraft und Formänderung,
die in allen statischen Konstruktionen besteht, ist dies möglich.
Mit meinen Objekten visualisiere ich diese sonst unsichtbaren
Vorgänge
und möchte sie bewußt machen.“
Walter Kaitna, 1979
Spannungsverhältnisse der verschiedenen Materialien sind Walter Kaitna aus seinem Beruf bereits seit langem vertraut, als er im Jahre 1962 beginnt, Skulpturen zu schaffen, um Kräfte – obwohl selbst nicht darstellbar – über ihre Wirkungen sichtbar werden zu lassen. Die Kräfte sollen dabei nicht – wie z. B. bei Wilhelm von Kaulbachs „Erzeugung des Dampfes“ – allegorisch dargestellt werden, sondern sie sollen real wirken. Da ungebundene Kräfte jedoch Bewegung erzeugen würden, steht zwangsläufig eine zweite Grundidee hinter Kaitnas Skulpturen: die Forderung nach einem Gleichgewicht der Kräfte.
Die Suche nach einem idealen Maß an Ausgewogenheit findet bereits in Skulpturen aus vorgeschichtlicher Zeit ihren Niederschlag: Viele für kultische Zwecke hergestellte Objekte (Idole von den Kykladen, Kreuzzeichen, Götterstatuen usw.) sind achsensymmetrisch angelegt – empfundenes und real vorhandenes Gleichgewicht sind hier noch an die gleiche Erscheinungsform gebunden. Erste Trennungen von objektiv überprüfbarem, mechanischem Gleichgewicht und nur noch subjektiv optisch wahrnehmbarem finden sich bereits im klassischen Altertum: So definierten z. B. die Pythagoräer ganzzahlige Verhältnisse bei den Abmessungen von Bauten, Skulpturen usw. als harmoniesteigernd. Im Mittelalter waren es z. B. die Fibonnacci-Zahlen und die Teilung nach dem Goldenen Schnitt, in den zwanziger Jahren Farb-Form-Untersuchungen am Bauhaus, mit deren Hilfe sich Menschen bei der Suche nach einem Maß für Schönheit und Harmonie in Kunstwerken sinnvolle Ergebnisse erhofften.
Kaitna schlägt einen neuen Weg über die Statik ein: Er berechnet Neigungen und Biegelinien von Stahlstäben so, daß sie sich über einem von ihm vorgegebenen Punkt treffen – sich das Gleichgewicht der Kräfte über dem vom Künstler erwählten Punkt einstellt.
Kaitna gibt sich jedoch nicht mit den im stabilen Gleichgewicht ruhenden dreidimensionalen Skulpturen, den „Kräftesystemen“ zufrieden, sondern versucht, deren Transformation in die zweidimensionale Ebene der Farbkompositionen und in das Eindimensionale der (zeitabhängigen) Musik. Dabei geht Kaitna weg von den vielfältigen Ansätzen in der ersten Hälfte dieses Jahrhunderts, Farben und Töne einander paarweise zuzuordnen. Er sucht einen neuen Weg über Analogien in den Strukturen der Farb- und Tonvorräte und findet sich damit im Einklang mit entsprechenden Strömungen in der modernen Wissenschaft.
Kräftesysteme
Kaitnas Idee, die bei den Kräftesystemen gegebene mechanische Ausgewogenheit über von ihm erfundene Analogien in Gestalt von Bildern ins Optische bzw. über musikalische Kompositionen ins Akustische zu übertragen, darf hier sicher als ein fruchtbarer und eigenständiger Neuansatz unter den in der Kunstgeschichte vielfältig vorhandenen Versuchen [3], Malerei in Musik bzw. Musik in Malerei zu übertragen, angesehen werden. Jedoch stellt bei Kaitna nicht der direkte Übergang von Musik zur „Malerei“ das eigentliche künstlerische Ziel dar, sondern der Übergang entsteht indirekt dadurch, daß Kaitna versucht, wesentliche Merkmale seiner mechanischen Kräftesysteme sowohl in Musik als auch in Farbkompositionen zu übertragen.
Um Kaitnas Leistung insgesamt in Ansätzen würdigen zu können, soll vorab schrittweise erkennbar werden, wo und wie sein ästhetisches Empfinden bereits bei der Konstruktion von Kräftesystemen formend wirkt und wie Kaitna auf die äußere Gestalt der Kräftesysteme Einfluß nimmt.
Die physikalischen Rahmenbedingungen lassen dem Künstler nur einen kleinen Spielraum für eigene Gestaltungen. Diesen weiß Kaitna jedoch weitgehend zu nutzen: Bei einem Kräftesystem kann der Künstler die geometrische Gestalt der Bodenplatte, die Anzahl der auf ihr zu montierenden Stäbe sowie die Anordnung der Bohrungen auf der Platte vorgeben. Darüber hinaus kann er die Art der Zusammenführung der Stäbe an der Spitze des Kräftesystems sowie die Ausmaße des gesamten Kräftesystems wählen. Insbesondere kann er den Punkt des Kräftesystems festlegen, in dem alle Kräfte gemeinsam angreifen sollen.
Zur Gestaltung der Kräftesysteme
Bei den ersten Kräftesystemen scheint Kaitna die Abmessungen der Bodenplatte willkürlich, vermutlich vor allem physikalisch-technischen Randbedingungen genügend, festgelegt zu haben. Im Zuge einer intensiven ästhetischen Durchgestaltung – auch persönliche Anregungen Richard Paul Lohses fließen ein – geht der Künstler jedoch ausschließlich zum quadratischen Format über. Im Gleichklang dazu ist eine immer perfektere materielle Gestaltung der Bodenplatte zu sehen: Finden sich anfangs auch grobgeschnittene Eisenplatten am Boden, so weichen diese im Laufe der Entwicklung mehr und mehr Aluminiumplatten mit glattgeschliffenen Rändern und polierten Oberflächen, sodaß schließlich das optisch verfeinerte Metall am Boden in Korrespondenz zur Eleganz der elastisch gebogenen Stäbe aus Edelstahl steht.
Die Position der Bohrungen auf der Bodenplatte gibt der Künstler vor: Dabei ist keine einheitliche künstlerische Strategie auszumachen. In allen Schaffensperioden treten unregelmäßig gebohrte Platten neben streng geometrisch strukturierten auf. Kaitna hat offenbar die verschiedenen Möglichkeiten, mit der Wahl der Bodenbohrungen das Erscheinungsbild des einzelnen Kräftesystems wesentlich zu beeinflussen, ausgelotet. Er hat sich jedoch nicht für ein bestimmtes Schema entschieden. Es gibt sogar ungewöhnliche Sonderfälle, wie z. B. die „Hommage à Josef Matthias Hauer“ (KS 247, 1981), bei der die Bohrungen einer Hauer’schen Trope entsprechend angebracht wurden.
Im Prinzip ist ein Kräftesystem bereits mit nur zwei Stäben realisierbar; dem Autor ist jedoch keines in dieser Art bekannt. Dagegen finden sich mehrfach Stabzusammenfassungen zu zwei gleichstarken Gruppen, die sich – wie zwei einzelne Stäbe es täten – an der Spitze treffen. Kräftesysteme mit für drei einzelne Stäbe oder für drei gleichstarke Stabgruppen regelmäßig verteilten Bohrungen (z. B. drei zu je vier, drei zu je fünf, drei zu je zwei usw.) fügt der Künstler am Boden zu einem dreizackigen Stern oder zu einem gleichseitigen Dreieck. Vier bzw. fünf Bohrungen sind in manchen Werken unregelmäßig am Boden angeordnet, sie können aber auch regelmäßig, genau in den vier Ecken eines bzw. in den Ecken und im Mittelpunkt eines Rechteckes, liegen.
Zwei einzelne Stäbe könnten sich nur in einer Spitze treffen, zwei gleichstarke Stabgruppen jedoch faßt der Künstler oben zu einer geraden Linie zusammen oder komprimiert sie zu zwei nebeneinander verlaufenden Linien und erzeugt dadurch den Eindruck, daß sich dort nur zwei Stäbe treffen.
Besitzt ein Kräftesystem dagegen drei Stäbe, so läßt Kaitna es in einer Spitze enden oder er verbindet die drei oberen Stabenden so, daß sich ein dreizackiger Stern oder ein gleichseitiges Dreieck ergibt. Sechs, neun oder zwölf Stäbe faßt Kaitna, ähnlich wie am Boden, in mehreren Beispielen zu gleichstarken Gruppen zusammen (drei Gruppen zu je zwei, drei oder vier Stäben), die dann wie drei einzelne Stäbe wirken können und oben einen dreizackigen Stern oder ein gleichseitiges Dreieck bilden. Die Formen am Boden und an der Spitze können verschieden ausfallen (z. B. am Boden das Dreieck und oben der Stern). Es gibt aber auch Kräftesysteme mit oben und unten gleicher geometrischer Grundform.
Auch bei aus vier Stäben konstruierten Kräftesystemen läßt Kaitna mehrere in sich geordnete Lösungen an der Spitze zu: dort können sich je zwei Stäbe treffen, oder sie treffen sich alle vier in einer Spitze. Fünf Stäbe – gleichgültig, ob sie am Boden regelmäßig von den Ecken und der Mitte eines Rechteckes ausgehen oder unregelmäßig in die Bodenplatte eingesetzt sind – läßt er immer in einer gemeinsamen Spitze enden; andernfalls hätte er einmal zwei und einmal drei Stäbe aufeinandertreffen lassen müssen und so ein im Vergleich zum physikalischen Gleichgewicht erstaunliches optisches Ungleichgewicht erzeugt.
Sieben Stäbe tragen ebenfalls von Natur aus das Ungleichgewicht in sich, wenn man nicht alle sieben oben zusammenfaßt. Kaitna spaltet die sieben am Boden in 2 + 2 + 3 auf, wobei allerdings vier davon am Boden auf einem Strahl angeordnet sind, während sich in der Spitze zweimal je zwei zu Paaren fügen, über denen sich ein Dreierdom wölbt.
Beim Zusammenfügen der Stäbe am oberen Ende gibt es demnach folgende grundsätzliche Variationsmöglichkeiten: Bei kleinen ungeraden Zahlen wählt Kaitna wegen der erwünschten Ausgewogenheit stets das Ende in einer einzigen Spitze. Bei durch drei teilbaren Anzahlen sieht der Künstler neben dem Zusammenwirken aller Kräfte in einem Punkt auch die Möglichkeit, sie in einem dreizackigen Stern oder in einem gleichseitigen Dreieck enden zu lassen. Bei geraden Anzahlen kann er zwei gleichgewichtige Spitzen einführen, z. B. vier Stäbe in zwei Paaren oder sechs Stäbe in zwei Trios enden lassen. Er kann aber auch die Stäbe auf zwei Gruppierungen verteilen, die er am oberen Ende in zwei geraden Stücken nebeneinander anordnet. Nie jedoch bilden sich oben Vierecke, wie er sie am Boden vielfach einsetzt. Schließlich bleibt Kaitna bei jeder Zahl noch die Möglichkeit, alle Stäbe in gleichen Abständen oder in progressierender Abstandsfolge auf einer gemeinsamen Geraden zu plazieren.
Allen Kräftesystemen gemeinsam ist: Nie enden die Stäbe irgendwo zufällig oder scheinbar zufällig angeordnet, denn eine der wesentlichen Entscheidungen, die der Künstler bei den Kräftesystemen treffen kann, besteht gerade darin, den Punkt bzw. die Punkte festzulegen, über denen alle Kräfte an der Spitze der Skulptur aufeinandertreffen sollen; oft fällt er mit dem Mittelpunkt der Platte zusammen. Dann erst kann er Neigungswinkel und Biegelinien der Stäbe mit Hilfe einer gewöhnlichen Differentialgleichung zweiter Ordnung berechnen. Als ein mit Methoden der Angewandten Mathematik vertrauter Ingenieur ist er dazu in der Lage: in seinen Aufzeichnungen notiert er mit Datum vom 25. März 1976 „Mathematische Grundlagen: Exakte Berechnung der Biegelinie“ und berechnet dort im Detail für die hier auftretenden Durchbiegungen jene Kräfte, die jeweils am oberen Stabende wirken. Insbesondere berechnet er für jeden Stab, unter welchem Winkel dessen Bohrloch in die Bodenplatte zu bohren ist, damit die Stabbiegungen am oberen Ende alle zum gleichen Punkt führen und sich dort alle (in einer waagrechten Ebene) auf die oberen Stabenden wirkenden Kräfte gegenseitig aufheben, so, daß das Kräftesystem im stabilen Gleichgewicht verharrt.
Kräftesysteme in der Gegenwartskunst
Das Erzeugen und Ausgleichen von optischen Spannungen bewegte bereits die Bildhauer des klassischen Altertums (z. B. Polyklet [1]). In der heutigen Skulptur wird, wie auch in anderen Bereichen der modernen Kunst, erfahrbar, daß die materielle Spannung an sich bereits wesentlicher Inhalt einer Skulptur sein kann. Einige Beispiele dazu mögen verschiedene mögliche Ansätze aufzeigen: Während Kaitnas unter Spannung stehende Kräftesysteme sich selbst im Gleichgewicht halten, bringen Künstler wie Naum Gabo und Henry Moore Verspannungen an bereits stabil vorgegebenen Skulpturen an. Max Bill schöpft ein viele Meter langes metallenes Möbius-Band, das von einer Raumdecke herabhängt. Die Schwerkraft dehnt es, bis sich das Gewicht des gewundenen Bandes und die entgegenwirkende Spannkraft im Gleichgewicht befinden.
Nahezu zeitgleich mit Kaitnas „Kräftesystemen“ entstehen Verschnürungen wie z. B. das „Rohrschnurstück auf weiß gestrichenem Brett“ (1981) von Alf Schuler, „Sigma Data“ (1976) von Kenneth Snelson und „Kubus“ (1972) von Jean d’Imbleval: geradlinige Eisenstäbe, metallene Winkel und Dreifußformen sind so gespannt, daß einige von ihnen zu schweben scheinen. Rainer Ruthenbeck steckt eiserne Platten in hängende Tücher, die sich unter der Last des Gewichtes eng an die in geometrischen Formen geschnittenen Eisenplatten anschmiegen. Aber dort, wo das nicht möglich ist, laufen sie – Kaitnas Stabbiegungen ähnlich – in weiten Bögen aus, wie man sie auch von hängenden Brücken aus dem südamerikanischen Urwald, vom Münchner Olympiadach, von Hochspannungsüberlandleitungen, von aufgestellten Strohgarben, von Helmut Bruchs an beiden Enden aufgehängter Metallstange als „Gravitationskurve“ her kennt. Manche Arbeiten von Herbert Oehm (z. B. „Spannplastik“ (1969)) kommen wegen der in ihnen spürbaren Kräfte den Durchbiegungen der Kaitna’schen Stäbe nahe, doch biegt er nicht Stäbe, sondern Acrylglasplatten, die von Nylonfäden gespannt werden. Soto wiederum montiert dünne Stahlstäbe senkrecht auf schwingende Untergründe, sodaß sich die Schwingungen der Untergründe in die Stäbe fortsetzen können, wo sich dann stehende Wellen mit „Bäuchen“ und „Knoten“ ausbilden können. Es gibt aber auch Arbeiten von ihm, in denen im Gleichgewicht aufgehängte Stäbe bei fast völliger Bewegungsfreiheit mit zwei freien Enden hin und her schwingen können, gewissermaßen einen Gegenpart zu Kaitnas aufeinanderwirkenden Stäben übernehmen könnten. Der englische Künstler Eric Snell schließlich spannt in seinen Installationen einen Faden, indem er zwei an den Enden befestigte Magnete einander anziehen läßt, bis die gesamte Konstruktion in einem stabilen Gleichgewichtszustand verharrt.
Während alle vorgenannten Künstler ebenso wie Kaitna der Schönheit der physikalisch-natürlichen Schmiegungen und Windungen den ihr angemessenen Entfaltungsspielraum lassen, gibt es andererseits auch Künstler, die den Betrachter gerade dadurch beunruhigen, daß sie ein ihm vertrautes physikalisches Gleichgewicht bewußt stören: Wolfgang Nestler z. B. hängt ein ausgeschnittenes Eisenstück an einem fast unsichtbaren Faden wieder passend in die ursprüngliche eiserne Ellipse so ein, daß das beunruhigende, optische Ergebnis eine schräg im Raum aufgerichtete elliptische Skulptur ist.
Strukturfelder
Schaut man senkrecht von oben auf ein Kräftesystem, das nur eine Spitze hat, so fallen die Stäbe des Systems optisch mit ihren senkrechten Schatten-Projektionen auf die Bodenplatte zusammen. Diese Abbildung eines räumlichen Kräftesystems in ein Strukturfeld in der Ebene fasziniert Kaitna. Ihn interessiert dabei vor allem die Gleichartigkeit der Kräfteverhältnisse bei der räumlichen Kräftesystem-Skulptur und ihrer Projektion in die Strukturfeld-Ebene auf der Bodenplatte: An der Spitze der Skulptur erzeugen die in der Horizontalen zusammenwirkenden Kräfte ein Gleichgewicht; in der Bodenplatten-Ebene verharren die zur Länge der Projektionen proportionalen Kräfte ebenfalls im Gleichgewicht und bilden dabei – senkrecht unter der Spitze – ein Gleichgewichtszentrum Z aus.
Diese Projektionen bieten Kaitna zunächst die bis dahin in der Kunst nicht genutzte Möglichkeit, räumlich wirkende Kräftesysteme in einer Ebene zu visualisieren. Im weiteren Verlauf seiner Arbeit gelangt der Künstler zu neuen abstrakten geometrischen Darstellungen, neuen Konstellationen in Strukturfeldern, denen nicht mehr immer eine reale Kräftesystem-Versuchsanordnung vorausgehen muß. Schließlich hat sich Kaitna soweit von den ursprünglichen physikalischen Vorgaben gelöst, daß er sich kombinatorischen Untersuchungen in Strukturfeldern zuwenden kann, vergleichbar etwa mit Sol Le Witts systematischer Suche nach allen möglichen „incomplete open cubes“.
Diesen von Kaitna kombinatorisch bestimmten und angeordneten und zu seriellen Bildern zusammengefaßten Strukturfeld-Folgen liegen bestimmte Gesetzmäßigkeiten zugrunde, die bei der Addition von Kräften gelten. Auf diese Regeln sei zunächst kurz eingegangen, ehe die künstlerischen Eingriffe, die Kaitna beim Übergang von einer Strukturfeld-Konstellation zur nächsten vornimmt, aber auch, wie weit das von ihm einmal vorgegebene System den weiteren Ablauf diktiert, hier erläutert werden.
Kräftepaare
Befestigt man fünf Zugfedern an verschiedenen Punkten auf einer Platte, zieht sie dann aus und schnürt sie an den Angriffspunkten zusammen, so wird sich ein Punkt (Z) finden, in dem sie alle gemeinsam so angreifen, daß sich ihre Kräfte gegenseitig aufheben, und das ganze System somit in Ruhe bzw. stabiler Lage verharrt. Da die Kraft mit der eine Feder wirkt, proportional zu ihrer Ausdehnung aus der Ruhelage ist, gibt die Entfernung des Aufhängepunktes (in den Abbildungen mit A, B, C, D, E bezeichnet) jeder Feder vom Zentrum Z ein Maß für die Stärke der wirkenden Kraft an.
Die von zwei Federn ausgeübten Kräfte (A, B) kann man durch eine resultierende Kraft ersetzen (Bild 1). Diese Kraft A+B ergibt sich als die resultierende Diagonale des von beiden Kräften aufgespannten Kräfteparallelogramms. Man kann sie aber auch erhalten, indem man die beiden Kräfte in eine horizontale und eine vertikale Komponente zerlegt, und beide komponentenweise addiert.
Kaitna hat nun – meistens von einer speziellen, aus einem realisierten Kräftesystem abgeleiteten Federinstallation ausgehend – auf folgende Weise viele verschiedene zum gleichen Zentrum Z gehörende Kräftekonstellationen gefunden (Bild 1): Je zwei der fünf in Z angreifenden Kräfte tauschen miteinander die vertikale Komponente (indem sie in einem Horizontal-Vertikallinien-System, in Kaitnas Strukturfeld, die Position auf den Horizontalen miteinander vertauschen – aus A wird dann A’ und aus B wird B’). Wie man erkennt, bleibt die resultierende Kraft A+B bzw. A’+B’ dabei unverändert; das Zentrum Z bleibt an seinem Ort (Bild 2).

Der Künstler hat nun alle Kräftekonstellationen notiert, die man erhält, wenn auf jeder waagrechten und senkrechten Linie genau ein Kräfteangriffspunkt (A, B, C, D, E) liegt. Unter diesen Bedingungen gibt es genau 5·4·3·2·1=120 verschiedene Kräftekonstellationen mit dem gleichen Zentrum Z [4]. Es ist nun besonders interessant zu verfolgen, wie systematisch Kaitna bei der Notation dieser vielen verschiedenen Kräftekonstellationen und bei den Übergängen von einer zur anderen Konstellation vorging. Und es wird sich zeigen, daß seine systematische Vorgehensweise ihn hier – wie in den anderen noch zu behandelnden Transformationen der Kräftesysteme – als einen streng determiniert, konkret arbeitenden Künstler ausweist ("Variationen – Werksnummer WNr. 130" weiter unten).
Übergänge
Die folgenden Erläuterungen zu Kaitnas Vorgehensweise sollen dem Betrachter seiner Werke helfen, zu beurteilen, wie sehr es Kaitna gelang, subjektive Entscheidungen weitgehend zugunsten objektiver, systemgebundener Abläufe zurückzuhalten, und somit die Schönheit der in sich ruhenden Kräftesysteme ohne persönliche Eingriffe und damit möglichst neutral in Strukturfeld-Bilder zu transformieren.
Kaitna führt die fortschreitende Veränderung der Kräftekonstellationen innerhalb eines Strukturfeldes nicht willkürlich durch, sondern befolgt dabei strenge Regeln. Ein gutes Beispiel hierfür bieten die „Variationen“, wie sie im Bild oben dargestellt sind: Zunächst legt der Künstler das Strukturfeld in einem Koordinatenraster fest. Hier besteht es aus fünf horizontalen und fünf vertikalen Linien. Überall dort, wo sich Vertikalen und Horizontalen kreuzen, kann der Angriffspunkt einer Kraft liegen.

Bemerkenswert ist bereits hier die völlig systematische Vorgehensweise des Künstlers beim Festlegen des ersten Zustandes (im ersten Feld links unten der o. a. Abbildung): Das Startfeld (Bild 3) zeigt die fünf Angriffspunkte der fünf Kräfte mit dem ersten Punkt (A) auf dem Kreuzungspunkt der ersten Horizontalen von unten mit der ersten Vertikalen von links. Die zweite Kraft greift am Kreuzungspunkt (B) der zweiten Horizontalen von unten mit der zweiten Vertikalen von links an, ... die fünfte am Kreuzungspunkt der obersten (fünften) Horizontalen mit der am weitesten rechts (fünften von links) stehenden Vertikalen.
Kaitna behält diese logische Strenge nun auch, soweit es möglich ist, beim Umwandeln von einem Gleichgewichts-Zustand in den anderen bei und schränkt damit seine Möglichkeiten, durch subjektive Entscheidungen in den Ablauf des Umwandlungsprozesses einzugreifen, wesentlich ein. Beim Übergang vom ersten zum zweiten (danebenstehenden) Zustand tauschen der erste und der zweite Angriffspunkt (in der Zeichnung mit A und B benannt) ihre Horizontalen, bleiben aber auf ihren ursprünglichen Vertikalen (Bild 4). Die von A und B gemeinsam auf das Zentrum Z wirkende resultierende Kraft bleibt erhalten, wie wir in den Vorüberlegungen sahen; ihre horizontale Komponente ist die ursprüngliche, da die Punkte A und B auf ihren Vertikalen bleiben. Die vertikale Komponente bleibt ebenfalls erhalten, da die in A und B angreifenden Kräfte ihre vertikalen Komponenten nur tauschen. Dem Künstler gelingt es somit, das Zentrum Z festzuhalten, obwohl zwei der fünf Kräfte sich änderten.
Kaitna hat sämtliche Verteilungen der fünf Angriffspunkte notiert, die zu (Gleichgewichts)Zuständen mit demselben Zentrum führen und damit das für ihn wichtigste Merkmal gemeinsam haben. Auch hier wählt er die Reihenfolge ihrer Notation nicht willkürlich aus, sondern unterwirft sich – wie die obigen ersten sechs Bilder zeigen – wiederum einem strengen Schema.
Zustand 1 nach Zustand 2: erste und zweite Kraft tauschen Horizontale
Zustand 2 nach Zustand 3: zweite und dritte Kraft tauschen Horizontale
Zustand 3 nach Zustand 4: dritte und vierte Kraft tauschen Horizontale
Zustand 4 nach Zustand 5: vierte und fünfte Kraft tauschen Horizontale
Zustand 5 nach Zustand 6: fünfte und erste Kraft tauschen Horizontale
Kräftefusionen
 |
links: Horizontale Kräftefusion – WNr. 229;
rechts: Vertikale Kräftefusion – WNr. 231, 1981 |
Am Beispiel einer „Kräftefusion“ (wie links dargestellt) soll hier der Weg verfolgt werden, auf dem Kaitna ein physikalisches Kräftesystem in ein farbiges Bild transformiert und dann schrittweise über Kräftefusionen die Anzahl der auftretenden Farben reduziert: Zunächst stellt Kaitna einen Farbkreis her. Dabei entscheidet er sich nicht für einen Kreis, bei dem sich die Farben kontinuierlich ändern, sondern er unterteilt ihn in 24 gleichgroße Intervalle, wobei die drei Grundfarben Gelb, Rot und Blau jeweils um einen Drittelkreis voneinander entfernt liegen (Bild 9).
In die Mitte dieses Farbkreises plaziert Kaitna das Zentrum Z eines in die Ebene projizierten Kräftesystems – im vorliegenden Beispiel besteht es aus fünf Stäben. Es ergeben sich fünf unterschiedlich lange und in verschiedene Richtungen zeigende Vektoren. Die Vektoren weisen jeweils auf ein Feld des Farbkreises und bestimmen so für jeden Vektor die Farbe, in die er transformiert werden soll. Zugleich gibt die Länge des Vektors an, wie groß der Anteil dieser Farbe in ihrer Bildhälfte sein soll. Ausgehend von dem im ursprünglichen Kräftesystem vorhandenen Gleichgewicht der Kräfte, definiert Kaitna entsprechend ein optisches Gleichgewicht der Farben, das dann in der entstehenden Farbkomposition auch vorhanden ist. Er erreicht dies, indem er den Kreis vertikal in zwei Hälften unterteilt. So steuert jeder Kräftepfeil über die ihm zugeordnete Kreishälfte nur Farben in der entsprechenden Bildhälfte bei (Bild 10). Auf eine sehr ausgeklügelte Weise reduziert der Künstler nun schrittweise die im Bild 11 auftretenden Farben, indem er Kräfte zu neuen Kräftekonstellationen fusioniert, die er dann wiederum in farbige Bilder überträgt.

Der Weg vom fünffarbigen zum vierfarbigen Bild: Zunächst zerlegt der Künstler den in Richtung ‘bg’ (blaugrün) weisenden Pfeil in eine grüne und eine blaue Komponente (Bild 12). Der blaue Anteil (1) verlängert den bereits zuvor vorhandenen blauen Pfeil ‘b’ und vergrößert dann in der linken Bildhälfte entsprechend den blauen Farbanteil. Der Pfeil ‘2’ in der linken Kreishälfte legt einen Grün-Anteil in der linken Bildhälfte fest. In der linken Kreishälfte handelt es sich bei diesem ersten Schritt nicht um eine Kräftefusion, sondern um eine Ersetzung von zwei Kräften durch zwei andere, während in der rechten Kreishälfte tatsächlich bereits eine Kräftefusion von drei zu zwei Kräften stattfindet (Bild 13):
Der der Farbe Rotorangeorange zugeordnete Pfeil (in Richtung ‘roo’) wird zerlegt in eine Komponente 1 in Richtung ‘r’ und eine Komponente 2 in Richtung ‘o’. Die Komponenten werden jeweils zu den bereits vorhandenen Farbpfeilen addiert (Bild 14). Analog dazu, entsteht im Farbbild aus einer dreifarbigen eine zweifarbige rechte Bildhälfte (Bild 15).
Im nächsten Schritt werden die zwei Pfeile ‘r’ und ‘b’ zu einem in Richtung ‘bv’ weisenden Pfeil fusioniert (Bild 16) und in einem zusätzlichen – physikalisch nicht unbedingt notwendig gewesenen – Schritt, verlängert der Künstler nun den Pfeil ‘o’. Das Gleichgewicht bleibt erhalten, weil er ein ebenso langes entgegengesetztes Stück ansetzt, das er jedoch in zwei Komponenten 1 (in Richtung ‘g’) und 2 (in Richtung ‘bv’) zerlegt (Bild 17).

Diese Komponenten addiert er zu den zu diesen Farben bereits vorhandenen Pfeilen und kommt zu einem Kräftesystem, in dem nun nur noch drei Pfeile – im Bild entsprechend nur noch drei Farben – auftreten (Bild 18 u. 19).
Die letzte Stufe der Kräftefusion – die Reduzierung auf zwei Kräfte – folgt nun beinahe automatisch. Zunächst ergeben ‘o’- und ‘bv’- einen ‘r’-Pfeil, der genauso lang ist wie der ‘g’-Pfeil (Bild 20 u. 21). Diese beiden Pfeile verlängert Kaitna im Gleichgewicht auf die Maximallänge.
Schließlich füllt Kaitna die entsprechenden Bildhälften ganz mit der jeweils zugehörigen Farbe (Bild 22 u. 23). Das Kräftesystem „KS 174“ ist eines der wenigen Beispiele, in denen Kaitna dazu kam, alle Transformationen vom ursprünglichen Kräftesystem über die kombinatorischen Abwandlungen des Strukturfeldes zu Tonfolgen und über Kräftefusionen zu Bildserien auszuführen.

Bereits hier zeigt die zur Kräftefusion gehörende Bildfolge wieder die schon im vorhergehend untersuchten Werk festgestellte Tendenz Kaitnas, optische Ruhe in die Bildfolge dadurch zu bringen, daß die Anzahl der von Zustand zu Zustand sich ändernden Farben möglichst klein gehalten wird, und zumindest eine der beiden Farben des Endzustandes bereits möglichst frühzeitig in den Einzelbildern auftritt: vom ersten zum zweiten (mittleren) bleiben die Farben Grün (‘g’) und GelbOrange-Orange (‘yoo’) erhalten, vom zweiten zum dritten Zustand müssen zwei Farben (‘g’ und ‘rv’) durch eine neue ersetzt werden, daher kann nur noch eine (‘yoo’) erhalten bleiben. Außerdem legt Kaitna mit ‘yoo’ bereits im ersten Zustand eine der beiden Farben fest, die später zum Endzustand gehören werden (Bild 24). Diese Farbe ist in allen Zuständen vorhanden und verbindet diese optisch miteinander.

Bild 24: Fusion zu Kräftesystem KS 174
Übertragung der Fusion von 4 zu 2 Kräften in Bilder mit 4 bis 2 Farben
Greifen an einem Punkt zwei Kräfte so an, daß Gleichgewicht herrscht, so sind sie entgegengesetzt gleich. Wenn Kaitna also von Kräftesystemen mit mehr als zwei Kräften ausgeht, die sich im Gleichgewicht der Kräfte befinden, und diese schrittweise so fusioniert, daß am Ende nur noch zwei im Gleichgewicht befindliche Kräfte übrigbleiben, so müssen diese entgegengesetzt gleich sein, d. h. im entsprechenden Kräftefusionsbild sind sie gleich lang und liegen beiderseits des Gleichgewichtszentrums Z auf einer Geraden. Transformiert Kaitna nun diesen Endzustand der Kräfte über den 24teiligen Farbkreis in ein Farbbild, so ergibt sich stets ein Bild, dessen Hälften in zwei Gegenfarben erscheinen. Dabei können diese beiden Endfarben wie im vorliegenden Beispiel Rot und Grün sein, es ist aber auch jedes andere Paar (Blau-Orange, Gelb-Violett usw.) denkbar. Kaitnas Transformation des physikalischen Kräftepaares führt also nicht zwangsläufig zu einem bestimmten Farbenpaar, sondern er hat hier die Möglichkeit auszuwählen.
Darin unterscheidet sich Kaitnas Ansatz wesentlich von vielen anderen Transformationsversuchen etwa von Tönen in Farben [3]. Und da das Endpaar vom Künstler wählbar ist – im vorliegenden Fall z. B. so, daß eine der fünf Farben (Rot) des Anfangszustandes auch im Endpaar auftritt –, bedeutet das auch für alle Farben der Zwischenzustände, daß sie im einzelnen vom Künstler subjektiv gewählt werden können. Und hier steuert der Künstler auch: Er bringt eine gewisse nachvollziehbare Kontinuität und optische Ruhe in die Bilderfolge einer Fusion. Er achtet darauf, daß in der Regel von einem Zustand zum nächsten nur eine Farbe verschwindet und sich bei den verbleibenden nur eine Farbe ändert. Nur beim Übergang vom ersten zum zweiten Zustand läßt der Künstler zwei Farben zugleich verschwinden und eine neue (das Grün des Endzustandes) dafür auftauchen. Damit sorgt er dafür, daß neben dem Rot auch schon das Grün des Endpaares sehr früh vorhanden ist und sich von Zustand zu Zustand weiter ausdehnen kann, um so dem ganzen Bild eine ruhige farbige Entwicklung von oben nach unten zu geben und es so farblich zu strukturieren.
Zusammenfassend kann man feststellen: Nach der Wahl aller Farben, die in einem Kräftefusionsbild auftreten sollen, liegt Kaitnas Bild in allen Einzelheiten, insbesondere in den einzelnen Farbflächengrößen, fest. Und offensichtlich sorgt gerade diese Festlegung der Farbflächengrößen durch Kaitnas objektives Transformationssystem dafür, daß alle Stufen eines Fusionsbildes optisch nahezu gleichartig auf den Betrachter wirken und damit eine ungewöhnliche Farbharmonie vom ersten bis zum letzten Zustand erzeugen.
Grundsätzlich gilt für Kaitnas Kräftefusionen und deren farbliche Darstellung:
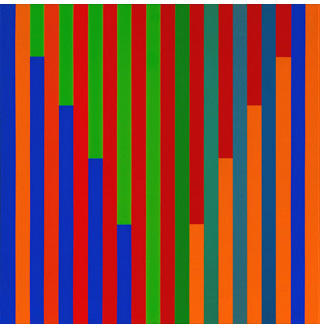 |
Übergänge – WNr. 273, 1982 |
- Jedes beliebige Paar von Gegenfarben kann für den Endzustand jeder von einem beliebigen Kräftesystem ausgehenden Kräftefusion ausgewählt werden.
- Jedes beliebige Kräftesystem – gleichgültig wieviel Stäbe vorhanden sind und wie sie zueinander stehen – läßt sich in das gleiche rot-grüne Schlußbild des obigen Beispiels fusionieren bzw. transformieren.
- Ein Rot-Grün-Bild kann – den Fusionsprozeß umkehrend – über Kräftezerlegungen in ein Bild übergeführt werden, in dem jede gewünschte Art und Anzahl von Farben aus dem Kaitna’schen Farbenkreis auftritt – dabei kann von mindestens einer Farbe sogar die Breite ihres Farbstreifens vorgegeben werden, während das System für andere die Breite ihres Farbstreifens festlegt.
- Jedes zweifarbige „Kräftefusionsbild“ kann – wie Kaitna es bei der schrittweisen Umwandlung eines Blauviolett-Gelborange-Bildes in ein Blaugrüngrün-Rotrotorange-Bild selbst vorstellt – in ein beliebiges anderes Gegenfarbenpaar-Bild übergeführt werden. Im Extremfall wäre das sogar in einem einzigen Schritt möglich – wenn er die zu den beiden Anfangsfarben gehörenden Pfeile jeweils in zwei den neuen Gegenfarben entsprechende Komponenten zerlegt. Hier stellt sich nun die Frage, worin die kreative Leistung des Künstlers unter diesen Umständen nach dem erstmaligen Finden der Fusions-Transformations-Ideen besteht, bzw. welcher Spielraum ihm als Künstler gegeben ist.
- In der formalen Gestaltung der einzelnen Zustände bzw. ihrer geschlossenen Darstellung besitzt Kaitna praktisch noch alle künstlerische Freiheit: Er kann die Zustände in Gestalt horizontal oder vertikal unterteilter Quadrate festhalten und diese zu einem geschlossenen Gesamtbild aneinanderfügen wie z. B. in den hier untersuchten „Kräftefusionen, 1981“. An die Stelle der Quadrate können aber auch hohe schmale Rechtecke treten, die aneinandergefügt den Prozeß der aufeinanderfolgenden „Übergänge“ (s. Bild oben) deutlicher werden lassen. Er nutzt aber auch die Möglichkeit, jeden Zustand zu einem eigenen Bild zu gestalten, wie er es bei den Farbkompositionen mit ineinandergefügten Quadraten überzeugend darstellt. Es ist bemerkenswert, daß Kaitna nicht die hier naheliegende Möglichkeit, kreisförmiger Bilder nutzt, sondern stattdessen ausschließlich auf die von fast allen konstruktiv arbeitenden Künstlern bevorzugten quadratischen bzw. rechteckigen Formate zurückgreift.
- Auch die farbliche Gestaltung seiner Bilder enthält noch viele künstlerische Freiheitsgrade: abgesehen von Drehungen und Spiegelungen, hat der Künstler etwa bei „Übergänge, 1981“ neben dem Weg über Gelb-Violett auch die Möglichkeit, Rot-Grün über Orange-Blau wieder in Rot-Grün überzuführen. Während bei dem tatsächlich gemalten Bild alle Farbabstufungen zwischen Gelb und Grün sowie zwischen Violett und Rot fehlen, würden beim zweiten möglichen Bild stattdessen die Farbabstufungen zwischen Blau und Violett sowie zwischen Orange und Gelb fehlen. Es gibt also bei gleichem formalen Aufbau und gleichem rot-grünen Anfangszustand zwei mögliche Konstellationen mit nahezu fließenden Übergängen. Bedenkt man nun noch, daß es insgesamt zwölf verschiedene Gegenfarben-Paare gibt, die den Anfangszustand eines solchen „Übergänge“-Bildes festlegen können, so erkennt man, daß hier 24 farblich wesentlich verschiedene Bilder möglich sind. Abgesehen von den, im Vergleich zu Lohses seriellen Bildern geringeren Anzahlen möglicher Bilder, kann man auch hier bei Kaitna von einem neuen, von ihm gefundenen Typ serieller Bilder sprechen, von denen er allerdings nur wenige realisiert hat.
Farbflächen im Quadrat
Kaitna hat fortwährend versucht, das physikalische Kräftegleichgewicht der Kräftesysteme in Bilder zu übertragen, die nach seinem ästhetischen Empfinden dem physikalischen Gleichgewicht entsprechend farblich und formal ausgewogen sein sollten. Bei der Festlegung der Farben und der Größe der mit ihnen zu bedeckenden Fläche geht er zunächst stets bei allen Visualisierungsversuchen (bei Fusionen, Übergängen usw.) in der gleichen Weise vor: Er stellt sich das Kräftesystem senkrecht in die Standebene projiziert vor. Die (schattenähnlichen) Bildstrecken der Stäbe auf der Bodenplatte bestimmen Farben und Farbflächen. Jedes Ende einer (Pfeil-)Strecke weist auf eine bestimmte Farbe in dem sie umgebenden 24teiligen Farbkreis; ihre Länge legt die zugehörige Farbfläche fest (Bild 10). Für die formale Anordnung der solchermaßen „automatisch“ bestimmten Farbverteilungen stehen Kaitna dann viele Möglichkeiten offen: Konzentrische Kreise hätten diese Aufgabe ebenso übernehmen können wie konzentrische Quadrate oder, wie im klassischen Altertum, auf einer gemeinsamen Grundlinie stehende Winkelformen oder, wie in Josef Albers’ „Interaction of Colour“, zwar nicht konzentrisch, aber dennoch ineinander angeordnete Quadrate usw.. Kaitna entscheidet sich für das Quadrat als Grundform mit einem einliegenden unversehrten Quadrat, um das sich drei jeweils gleichschenklige, zu Quadraten ergänzbare, Winkelflächen anordnen.

Bild 25a, b und c:
Einige gebräuchliche Methoden der Ineinanderschachtelung von Quadraten
Die Anordnung der Winkelflächen erfolgt nicht auf eine der bereits aus dem klassischen Altertum überlieferten Weisen (Bild 25), sondern alternierend: Beginnend mit dem innenliegenden Quadrat für die erste Farbe (Farbfeld 1, Bild 26), berechnet Kaitna die Breite der zur zweiten Farbe gehörenden winkelförmigen Fläche. Diese, ergänzt um das kleine Quadrat, bildet wieder ein Quadrat (Farbfeld 2, Bild 27). Das winkelförmige Element für die dritte Farbe berechnet er wieder derart, daß es mit den bereits farbigen Bildteilen ein Quadrat bildet, fügt die neue Fläche jedoch alternierend zur vorhergehenden auf der gegenüberliegenden Seite an (Farbfeld 3, Bild 28). Die vierte Fläche setzt Kaitna dann wieder auf der gegenüberliegenden Seite an (Farbfeld 4, Bild 29).
 |
Strukturelle Farbordnung – WNr. 213, 1980 |
Diese komplexe Anordnung der Farbflächen unterscheidet sich wesentlich von der Regelmäßigkeit der oben zitierten, nach überlieferten Methoden möglichen Bilder (Bild 25). Dennoch: Mit dem quadratischen Bildformat, der Orthogonalität, dem Auftreten eines inneren Quadrates und der für den Betrachter gegebenen Möglichkeit zur quadratischen Ergänzung aller Bildelemente enthält der formale Bildaufbau Kaitnas immer noch auffallend viele Ordnungselemente. Für eine bestimmte Farbflächenverteilung einer Serie, z. B. für ‘Pos.1 ‘, sind 24 Bilder in voneinander abweichenden Farben möglich, je nachdem wie Kräftesystem und Farbkreis zueinander gedreht werden (z. B.: "Strukturelle Farbordnung" – WNr. 213, 1980). Jedesmal, wenn etwa die größte der vier Strecken auf eine der 24 Farben des Farbkreises weist, legen die drei anderen Strecken zugleich die restlichen drei Farben fest.

(Die Farben durchlaufen alle Farbfelder phasenverschoben in der gleichen Reihenfolge
(hier für die Farben A und B dargestellt.)
In seiner weiteren Arbeit findet Kaitna zu vier formalen Variationen: Jedes der vier Bilder der Serie besitzt vier Felder für die Farben. Vertauscht man die vier von Kaitna mit A, B, C, D bezeichneten Farben zyklisch, so ergeben sich genau vier Variationen, die er in dieser Reihenfolge in die Farbfelder 1, 2, 3 und 4 einbringt:
| Farbfolge: |
ABCD |
BCDA |
CDAB |
DABC |
Farbfeld: |
1234 |
1234 |
1234 |
1234 |
Das bedeutet, daß die Farben der Serie von Bild zu Bild ihre Plätze zyklisch tauschen. Da ihnen jedoch nach Kaitnas vorhergegangenen Berechnungen verschieden große Flächen zustehen, bleibt zwar der formale Aufbau im wesentlichen bei allen vier Positionen der gleiche, die Größenverhältnisse schwanken jedoch. Die Bilder 31 und 32 zeigen am Beispiel der Farben A und B, wie diese beiden (ebenso wie die Farben C und D) nacheinander von Position zu Position die Farbfelder in der gleichen Reihenfolge durchlaufen: Die unterschiedlich großen, für die einzelnen Farben vorgesehenen Flächen führen „automatisch“ zu Bildern, die von Position zu Position verschieden wirken, obgleich der formale Aufbau im Prinzip erhalten bleibt. Damit gelingt Kaitna bei dieser Serie auf streng systematischem Wege eine erstaunliche Variationsbreite des Erscheinungsbildes. Kaitna verstärkt diesen Variationsreichtum noch durch Farbänderungen, die aber zugleich so behutsam vorgenommen werden, daß der Zusammenhang zwischen den verschiedenen Bildern der Serie gewahrt bleibt: Er dreht den Farbkreis, der ganz am Anfang die ersten vier Farben von ‘Pos.1’ bestimmte, von Position zu Position um ein einziges Feld weiter. Dadurch werden alle vier Farben jeweils durch ihre benachbarte im Farbkreis ersetzt.
Vertikale Transformationen
Kaitna hat ständig nach neuen Wegen gesucht, die dreidimensionalen Kräftesysteme in Bilder zu transformieren. Ein weiteres, von allen vorhergehenden wieder signifikant abweichendes Beispiel dafür stellen die Vertikalen Transformationen aus dem Jahre 1981 dar. Hier hat Kaitna erstmals einen Weg gefunden, auf dem er von den streng orthogonalen Flächenaufteilungen zu kurvigen Grenzverläufen hätte weitergelangen können: Er unterlegt dem Kräftesystem wieder ein Strukturfeld (Bild 3 ff.), auf dessen Kreuzungspunkten Farben notiert sind. Während das Kräftesystem sich über dem Strukturfeld dreht, weisen die Kraftpfeile nicht immer alle gleichzeitig auf neue Kreuzungspunkte und damit auf neue Farben wie im Farbkreis, sondern springen in unregelmäßigen Abständen auf neue Zustände über. Dadurch erzielt der Künstler bereits wesentliche Ordnungsstrukturen für diese Arbeiten: Von den drei Farben eines Bildes, das zu einem dreistäbigen Kräftesystem gehört, können in der Regel zwei erhalten bleiben, während nur die dritte Farbe wechselt. Bei den Transfusionen waren solche Zustandswechsel unmöglich; es mußten immer mindestens zwei Vektoren zu einem oder mehreren neuen Vektoren fusioniert bzw. im Bild mindestens zwei Farben durch eine oder mehrere neue ersetzt werden.
Darüber hinaus zeichnen sich diese Bilder dadurch aus, daß im Unterschied zu allen anderen Transformationsversuchen Kaitnas hier kleingestufte, fast schon geschwungen erscheinende Farbverläufe auftreten. Dieses beinahe schon kontinuierliche Zu- und Abnehmen der Farbstreifen erreicht der Künstler auf folgende Weise (Bild 33):
 |
Bild 33: Farbflächen ändern ihre Größe in kleinen Schritten in Abhängigkeit von der Länge der ‚Pfeil‘-Strecke, die das Gleichgewichtszentrum mit der Farbnummer auf der Feldlinie verbindet |
 |
Vertikale Transformation – WNr. 287, 1983 |
Der über die Strukturfeld-Linie streifende Pfeil legt neue Farben und – entsprechend der Pfeillänge bis zur Feldlinie – in kleinen Schritten zu- bzw. abnehmende Farbflächen fest. Der Anteil der einzelnen Farben an einem Querstreifen (z. B. in. „Horizontale Transformation – Variation mit Übergängen“ vom 12.12.1981) bestimmt sich aus dem Verhältnis der drei Pfeillängen dieses Zustandes zueinander.
Mit diesen Arbeiten war Kaitna einen wesentlichen Schritt hin zu kontinuierlich und kurvig verlaufenden Farbflächen gelungen: Da die Pfeile in beliebig kleinen Winkelschritten gedreht werden können, hätte er nun die Möglichkeit gehabt, beliebig kleinstufige, d. h. für das Auge praktisch kontinuierlich verlaufende Farbfelder zu erhalten. Dies ist eine für einen konkret-konstruktiv arbeitenden Künstler ungewöhnliche Bildkonzeption, da die diese Kunstrichtung geradezu kennzeichnende Geradlinigkeit aller auftretenden Linien sich hier relativiert hätte.
Tonreihen
Im zwanzigsten Jahrhundert existieren viele Ansätze, Musik in Malerei zu transformieren bzw. zu Bildern adäquate musikalische Werke zu komponieren [3]. Viele Komponisten vertonten Werke der bildenden Kunst [10]. Diese Vertonungen erfolgten in aller Regel intuitiv, nach nicht objektiv nachvollziehbaren Methoden. Anders verhält es sich dagegen bei vielen Versuchen, die den umgekehrten Weg gehen: Da gibt es zum einen den Ansatz, die Noten nicht einfach in üblichen Zeilen zu notieren, sondern sie in Gittern, auf Kreisbahnen, mit Stabdiagrammen und ähnlichen Veranschaulichungen aus Mathematik und Technik zu schreiben. Hierbei handelt es sich a priori nicht um neue Schöpfungen, sondern im wesentlichen sind es Umkodierungen der Notenschrift in geometrisch interessantere Darstellungen (als würde etwa ein in lateinischer Schrift gegebener Zeitungstext in Blindenschrift oder Morsezeichen umgewandelt). Teilweise finden sich derartige Ansätze u. a. in Werken von Hans Hinterreiter, Alfred Jensen, Rune Mields, Jakob Weder [3].
Auf einer anderen Stufe anzusetzen sind die vielen Vorschläge, jedem musikalischen Ton eine Farbe zuzuordnen. Strübin ordnet z. B. für jedes Musikstück in stets neuer subjektiver Festlegung jedem Ton eine Farbe zu. Dabei kann es durchaus vorkommen, daß einander benachbarte Töne auf dem Ittenschen Farbkreis weit voneinander entfernten Farben zugeordnet werden. Eine wichtige Erweiterung dieses Vorgehens besteht zum Beispiel in den Arbeiten von Severini und Wyschnegradsky, indem sie nicht mehr einzelnen Tönen Farben zuweisen, sondern mit einer Zuordnung von ganzen Tonskalen zu Farbskalen arbeiten. Teilt man dann das Farbspektrum in zwölf Farben auf, so läßt sich zur 12teiligen chromatischen Tonskala eine 12teilige Farbskala zuordnen, die das (Farb-)Spektrum durchwandert und wie die Tonskala in ihren Anfang zurückläuft. Hans Kayser hat, von einem derartigen Farb-Tonsystem ausgehend, eine weit differenziertere Tontabelle entwickelt, die jedoch wegen der am Anfang stehenden, subjektiv erfolgenden Tonleiter-Farbskala-Zuordnung in ihrem Erscheinungsbild ebenfalls individuell geprägt bleibt.
Kaitna hat hier nun einen völlig neuen Zugang zu Ton-Farbbeziehungen gefunden:
 |
Klangbild: Variation und Notation
WNr. 212 zu Tonreihe TR 45/Kräftesystem KS 174, 1981 |
Zunächst einmal werden Ton und Farbe nicht unmittelbar zueinander in Beziehung gesetzt. Gemeinsamer Ausgangspunkt für Transformationen in bildnerische oder musikalische Kompositionen ist jeweils ein (physikalisches) Kräftesystem. Das Kräftesystem wird auch hier in seiner in die Ebene projizierten Fassung (Bild 3 ff.) verwendet, doch werden jetzt von den Angriffspunkten der Kräfte Saiten zum Gleichgewichtszentrum gespannt: „Die Konstellation der formbildenden Kräfte eines Objektes (Anm. d. Verf.: eines Kräftesystems), als entsprechende Saitenspannungen dargestellt, ergibt ein Tonintervall mit adäquatem Intervallverhältnis ... Mit fortschreitender Veränderung der Kräftekonstellation innerhalb des Strukturfeldes entstehen Tonreihen, die elektronisch realisiert werden“ (Walter Kaitna [6]).
Bereits bei den Transformationen der Kräftesysteme in Bildwerke wird das intensive Bemühen des Künstlers um Objektivität bei der Festlegung der Farben durch die verschiedenen von ihm erfundenen Verfahren deutlich. Auch hier, bei der Umwandlung der Kräftesysteme in musikalische Kompositionen in Form von Sinusschwingungen, zeichnet sich Kaitna durch einen ungewöhnlichen und zugleich einleuchtenden Vorschlag aus: Wir sind bereits bei den Bildern auf Strukturfeld-Abfolgen gestoßen und haben dabei herausgefunden, daß es Kaitna gelungen ist, alle Strukturfeld-Konstellationen, die möglich sind, nacheinander so zu durchlaufen, daß die zu einem fünfstäbigen Kräftesystem entstehenden Zustände sich beim Übergang von einem Zustand in den nächsten stets nur in zwei Kräften ändern. Am Ende gelingt es ihm sogar, den letzten Zustand (rechts unten der in der Abbildung „Variationen, Werksnummer 130" abgebildeten Tafel aller 120 Zustände) so zu gestalten, daß er ebenfalls nur unter Abänderung von zwei Kräften wieder in den ersten Zustand (links oben) übergeht.

×
![]()
Variationen – Werksnummer WNr. 130, 1978↩
Da Kaitna dieses Modell auch für die musikalischen Transformationen einsetzt, ergeben sich hier analoge Lösungen und auch analoge Probleme. Er selbst notiert zu der Zeit in seinen Aufzeichnungen: „Es gibt viele Möglichkeiten, um ein Paar zu vertauschen“. Bei diesen Vertauschungen arbeitet er, wie bei der Übertragung der Kräftesysteme in Bilder, intensiv an der Überwindung des Problems, die strenge Gesetzmäßigkeit der Übertragung einzuhalten und dennoch genügend abwechslungsreiche, seinen ästhetischen Ansprüchen genügende Variationen in die Kompositionen einzubringen. Die künstlerische Anspannung, unter der er dabei zeitweise steht, zeigen knappe Notizen, die er noch wenige Tage vor der ersten Realisierung von „Dreiklängen“ nach einem Kräftesystem (23. Mai 78) zu den vorhergehenden Entwürfen anmerkt, so etwa am 14. Mai: „zu nahe“ und für die Ausführung nicht brauchbar. Die Koordinaten müssen weiter weg vom Zentrum liegen (sonst werden die Saiten zu kurz)“. Oder am 16. Mai: „zu wenig differenziert“. Innerhalb kürzester Zeit folgen auch hier die verschiedensten Ansätze, Redundanz und Komplexität der Kompositionen in ein, seinem Empfinden nach ausgewogenes Verhältnis zu bringen. Kaitnas Ansatz, auch die Hauer’schen Tropen hier einzusetzen, wird von ihm nicht weiter verfolgt; das bereits ungewöhnlich stark in ein Regelsystem eingefügte Zwölfton-Konzept, zusätzlich zu Kaitnas strengen Regeln in eine Komposition eingebracht, hätte notgedrungen zu ungewöhnlich hoher Redundanz geführt.
Zwei Beispiele aus seinen Aufzeichnungen mögen stellvertretend für seine vielen Kompositionsansätze dazu stehen und die Regelmäßigkeiten andeuten, die Kaitna hier, wie bei den Bildern, zur Erhöhung der Redundanz nutzt: In einer Komposition mit 24 Takten zu je vier Tönen, wobei jeder Ton vier verschiedene mögliche Tonhöhen besitzt und somit insgesamt 16 = 4·4 verschiedene Höhen, hat es Kaitna verstanden, die Tonhöhenfolgen bei jedem der vier Töne einer strengen Gesetzmäßigkeit – nur selten durch subjektive Eingriffe variiert – zu unterwerfen, wie sie am Beispiel des ersten Tones deutlich werden, der seine Tonhöhen in folgender Weise systematisch durchläuft:
Zahlenreihen zu einem Kräftesystem mit vier Stäben (24 Variationen/Takten):
Tonhöhen des ersten Tones

Oder, er hält (bei fünf Tönen) jeden Ton in zyklischer Folge für drei Takte auf gleicher Höhe.

Die nach Kaitnas System komponierten Werke zeigen, bedingt durch die in ihnen enthaltenen logischen Regeln und Bindungen, in gleicher Weise wie viele Zwölftonkompositionen, die Tendenz zu einem in sich geschlossenen, trotz der vorhandenen Variationen in seiner akustischen Wirkung auf den Hörer, ungewöhnlich einheitlich anmutenden Tongefüge.
Resümee
Nur einem Künstler mit dem Wissenshintergrund Kaitnas war es gegeben, zugleich Skulpturen seinen eigenen ästhetischen Vorstellungen zu unterwerfen (etwa im Hinblick auf die Lage des Gleichgewichtszentrums) und den darin enthaltenen Stab-Elementen dennoch die Freiheit natürlich-physikalischer Durchbiegung zu lassen. Das Geheimnis der Schönheit und Eleganz dieser Skulpturen liegt sicher in diesem Zusammenwirken von ästhetischem Gestalten und logischem Beherrschen der physikalischen Komponenten der Kräftesysteme. Kaitnas „malerisches“ Werk ist geprägt von der Suche nach der für ihn optimalen Lösung seiner sich selbst gestellten zentralen Aufgaben:
Wie kann man physikalisches Gleichgewicht in Farbkompositionen übertragen?
Wie lassen sich die Kräftesysteme – Skulpturen aus aufeinander Kraft ausübenden und sich gegenseitig im Kräftegleichgewicht haltenden Stäben – in Bilder transformieren?
In einem für das Entstehen eines Lebenswerkes wahrhaft knappen Zeitraum von wenig mehr als zehn Jahren, insbesondere in seinen letzten Lebensjahren, kommt ihm eine Fülle an Ideen dazu, die er zumindest noch in exemplarischen Kunstwerken umsetzen kann:
- Fusionen führen in Serien aufeinanderfolgender Zustandsbilder jede Farbkonstellation in ein gewünschtes Farbenpaar über.
- Übergänge bieten zur Bildmitte hinschwingende und auf dem Weg zum gegenüberliegenden Bildrand – physikalisch-quantitativ gleich, aber qualitativ im farblichen Erscheinungsbild verschieden – wieder zurückschwingende Farbverläufe.
- Positionen für ineinandergeschachtelte Quadrate (Strukturelle Farbordnungen) in durch ein Kräftesystem vorgegebenen Farben und Flächen findet Kaitna jeweils in atemberaubender Variationsbreite.
- Vertikale Transformationen öffnen Kaitna den Weg zum nicht mehr streng waagrecht-senkrecht erscheinenden Bildaufbau, auf dem er noch wichtige erste Bilder realisieren konnte – nur noch einen kleinen Schritt von der Entstehung der bereits erdachten Farbkompositionen mit nahezu kontinuierlichem Farb- und Kurvenverlauf in optischer Nähe zu den eleganten Biegungen der Stäbe entfernt.
Bei allen Bildideen zur Umwandlung von physikalischem Gleichgewicht in malerisches, besticht das Bemühen Kaitnas, seinen Weg zwischen objektiv gegebenen und überprüfbaren Transformationstechniken und seinem subjektiven ästhetischen Empfinden zu finden.
Die musikalischen Kompositionen entstehen aus dem gleichen Bemühen. Dabei findet Kaitna eine Übertragung aus dem Physikalischen ins Musikalische, die nicht (wie bei früheren Versuchen anderer Komponisten und Künstler) zu einer Festlegung von Einzeltönen führt, sondern das gesamte Tonfolgensystem festlegt, das dann relativ zu einem Grundton insgesamt verschoben werden kann. Neu an diesem Ansatz ist das, wegen der in Kaitnas Versuchsanordnung beliebig möglichen Saitenspannungen, entstehende kontinuierliche Frequenzspektrum, dessen Töne erst in unserer Zeit technisch realisierbar geworden sind.
Als in der modernen Kunstgeschichte einzig muß Kaitnas in beiden Richtungen begehbarer Weg der Transformation von Bildern in Tonreihen über ein physikalisches Zwischenglied – die Kräftesysteme – eingestuft werden.
Literatur
[1] Beck, H., Bol, P. C., Bückling, M. (Hrsg.): Polyklet (Katalog).
Museum alter Plastik, Frankfurt am Main, 1990.
[2] Bogner, Dieter: Musik und bildende Kunst in Wien. In: Maur, Karin v.:
Vom Klang der Bilder (Katalog). Staatsgalerie Stuttgart, 1985, S. 346 ff.
[3] Guderian, Dietmar: Serielle Strukturen und harmonikale Systeme. In:
Maur, Karin v.:
Vom Klang der Bilder (Katalog). Staatsgalerie Stuttgart, 1985, S. 434 ff.
[4] Guderian, Dietmar: Mathematik in der Kunst der letzten dreißig Jahre.
edition galerie lahumière, Paris und Bannstein Verlag, Ebringen/Br., 1990.
[5] Loef, Carl: Farbe Musik Form. Verlag Musterschmidt Göttingen, 1974.
[6] Kaitna, Walter: Kräftesysteme (Katalog). Wien, 1982.
[7] Kayser, Hans: Lehrbuch der Harmonik. Zürich, 1950.
[8] Maur, Karin v.: Musikalische Strukturen in der Kunst des 20. Jahrhunderts.
In: Maur, Karin v.: Vom Klang der Bilder (Katalog). Staatsgalerie Stuttgart, 1985, S. 3ft.
[9] Mazzola,: Die Geometrie der Töne. Verlag Birkhäuser Basel, 1991.
[10] Schneider, Klaus: Vertonte Gemälde. In: Maur, Karin v.:
Vom Klang der Bilder (Katalog). Staatsgalerie Stuttgart, 1985, s. 452 ff.
* Prof. Dipl.Math. Dietmar Guderian; Studium der Mathematik, Physik und Kunst; Wissenschaftlicher Mitarbeiter der DFVLR – Institut für Angewandte Mathematik und Mechanik und Professor an der Uni Freiburg; Spezialgebiete: Mathematik und Informatik und ihre Didaktiken, Mathematik in der Kultur – insbesondere der Kunst – der Gegenwart;Autor, Referent, Kurator, Ausstellungsmacher, Mitglied bzw. Juror verschiedener Stiftungen.
Dieser Text wurde
publiziert in: Walter Kaitna – Kräftesysteme 1962-1983. Hrsg.: Kunstraum Puchberg, Wien 1994
(S. 101-122) |

|
|